Cómo la teoría de cuerdas ayuda a descifrar el código oculto de las redes naturales
Durante décadas, los científicos han intentado explicar por qué las neuronas, los vasos sanguíneos o las ramas de los árboles se organizan como lo hacen. Ahora, un estudio en la revista Nature recurre a la teoría de cuerdas —una de las ideas más abstractas de la física— para descifrar el código geométrico que comparten las redes de la vida.
Por Enrique Coperías, periodista científico
Una misma geometría, dos mundos. Las ramificaciones de un árbol y las superficies abstractas de la teoría de cuerdas comparten principios matemáticos comunes: según un nuevo estudio, las redes naturales minimizan su coste material siguiendo reglas geométricas de superficie, no solo de longitud. Crédito: IA-DALL-E-©RexMolón Producciones
Científicos de disciplinas tan distintas como la neurociencia, la botánica o la física han compartido desde hace tiempo una intuición común: las redes que recorren la naturaleza, desde las neuronas del cerebro hasta los vasos sanguíneos o las ramas de un árbol, están diseñadas para ahorrar materia prima.
Cuanto menos cable se use, mejor. Esa idea, conocida como el principio de optimización del cableado, ha servido para explicar por qué las redes biológicas tienden a ramificarse de determinadas maneras. Sin embargo, un nuevo estudio publicado en la revista Nature sugiere que esa explicación se queda corta.
Para entender de verdad cómo se construyen estas redes, los investigadores han tenido que recurrir a una herramienta inesperada: la teoría de cuerdas.
Qué son las redes naturales y por qué importan
El trabajo, liderado por el físico Albert-László Barabási y su equipo en el Network Science Institute de la Universidad de Northeastern (Estados Unidos) propone un cambio profundo en la forma de plantear y abordar las redes físicas. En lugar de tratarlas como simples líneas que conectan puntos —una abstracción matemática muy útil, pero incompleta—, los autores sostienen que hay que considerarlas como lo que realmente son: estructuras tridimensionales con grosor, superficie y continuidad física.
🗣️ «Estábamos tratando estas estructuras como si fueran diagramas de cables —explica Xiangyi Meng, físico del Instituto Politécnico Rensselaer y primer autor del estudio. Y añade en un comunicado de esta institución—: Pero no son cables finos, son objetos físicos tridimensionales con superficies que deben conectarse de forma suave».
Y al hacerlo, descubren que las reglas clásicas que supuestamente gobiernan el diseño de las redes naturales se rompen de forma sistemática.
Qué es el árbol de Steiner
Durante décadas, el modelo dominante para describir estas redes ha sido el llamado árbol de Steiner, nombrado así en honor al matemático suizo Jakob Steine. Se trata de una solución matemática que minimiza la longitud total de los enlaces entre varios puntos. Según este modelo, cuando una red se ramifica, siempre lo hace en bifurcaciones perfectas: un cable se divide en dos, formando ángulos simétricos de 120 grados, todo en un mismo plano.
Este patrón aparece, por ejemplo, en el diseño idealizado de circuitos o tuberías. También se ha utilizado para describir las neuronas, los vasos sanguíneos o las raíces de plantas.
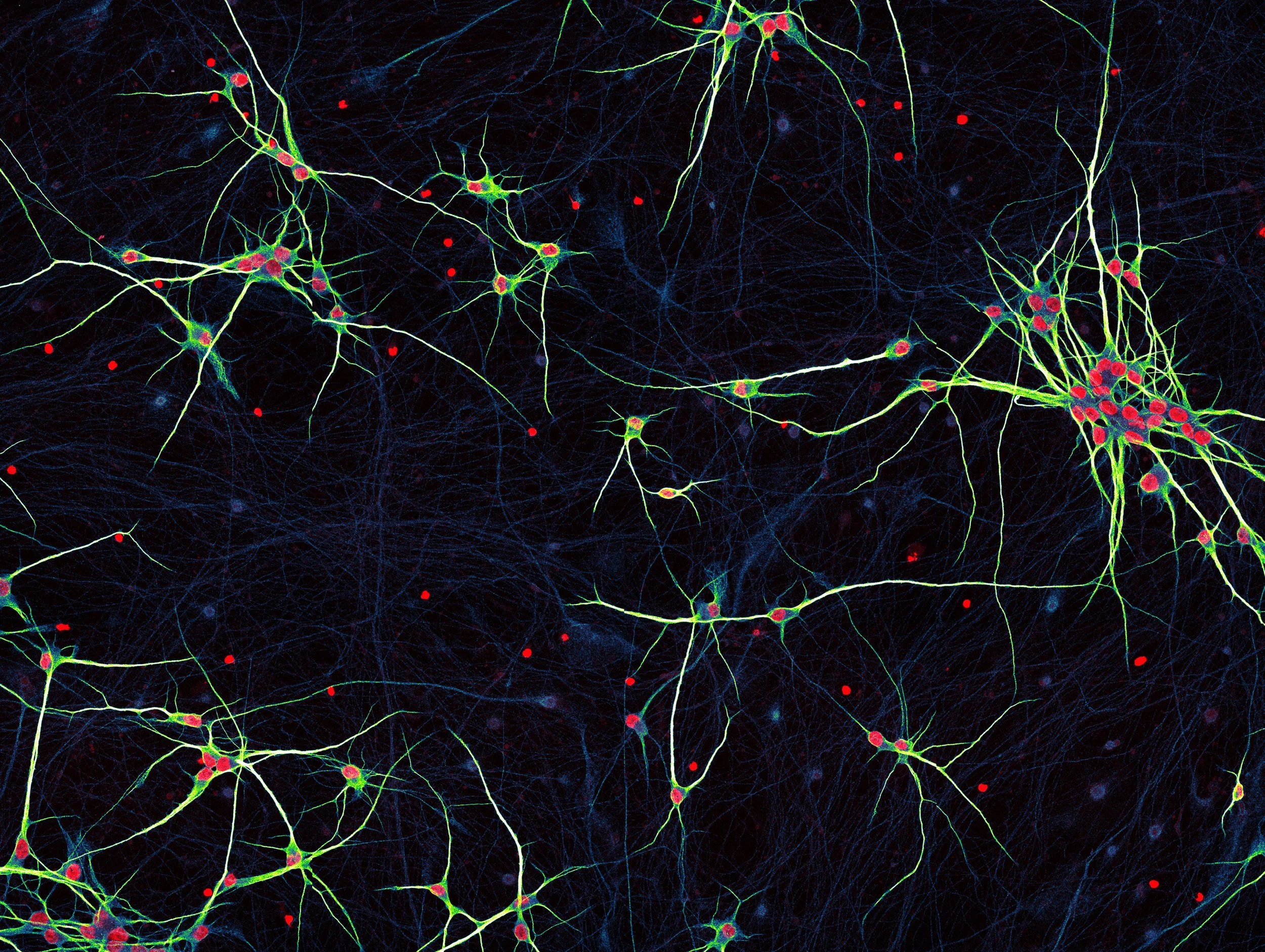
El problema es que, cuando los investigadores han podido observar estas redes con suficiente resolución, gracias en gran medida a los avances recientes en microscopía y reconstrucción tridimensional, han comprobado que la realidad es mucho más desordenada. Analizando seis tipos de redes físicas distintas, entre ellas neuronas humanas y de mosca, vasos sanguíneos, corales, árboles tropicales y plantas modelo como la Arabidopsis, el equipo de Barabási ha encontrado desviaciones claras y repetidas de las predicciones del modelo clásico.
La teoría de cuerdas puede ayuda a los neurólogos a conocer con mayor profundidad cómo se ramifican las neuronas humanas para crear redes. Cortesía: Dr. Saikat Ghosh / National Institutes of Health (NIH) / NICHD
Por qué el modelo clásico de optimización del cableado falla
Por ejemplo, no es raro encontrar trifurcaciones, puntos en los que una rama se divide en tres en lugar de dos. Tampoco es excepcional que las ramas no estén en un mismo plano, o que los ángulos entre ellas sean muy desiguales.
En algunos casos, una rama parece brotar de forma perpendicular de otra, formando un ángulo cercano a 90 grados, algo que las teorías tradicionales no pueden explicar sin recurrir a excepciones ad hoc.
Pero ¿por qué falla el modelo? Según los autores, porque parte de una simplificación excesiva: trata las redes como si fueran líneas sin grosor. Pero en el mundo real, los cables, los vasos y las ramas tienen volumen, superficie y deben unirse de forma suave, sin esquinas imposibles ni discontinuidades físicas. Si se tiene en cuenta ese coste adicional —el de construir y mantener superficies tridimensionales—, el problema matemático cambia por completo.
Qué aporta la teoría de cuerdas a la biología
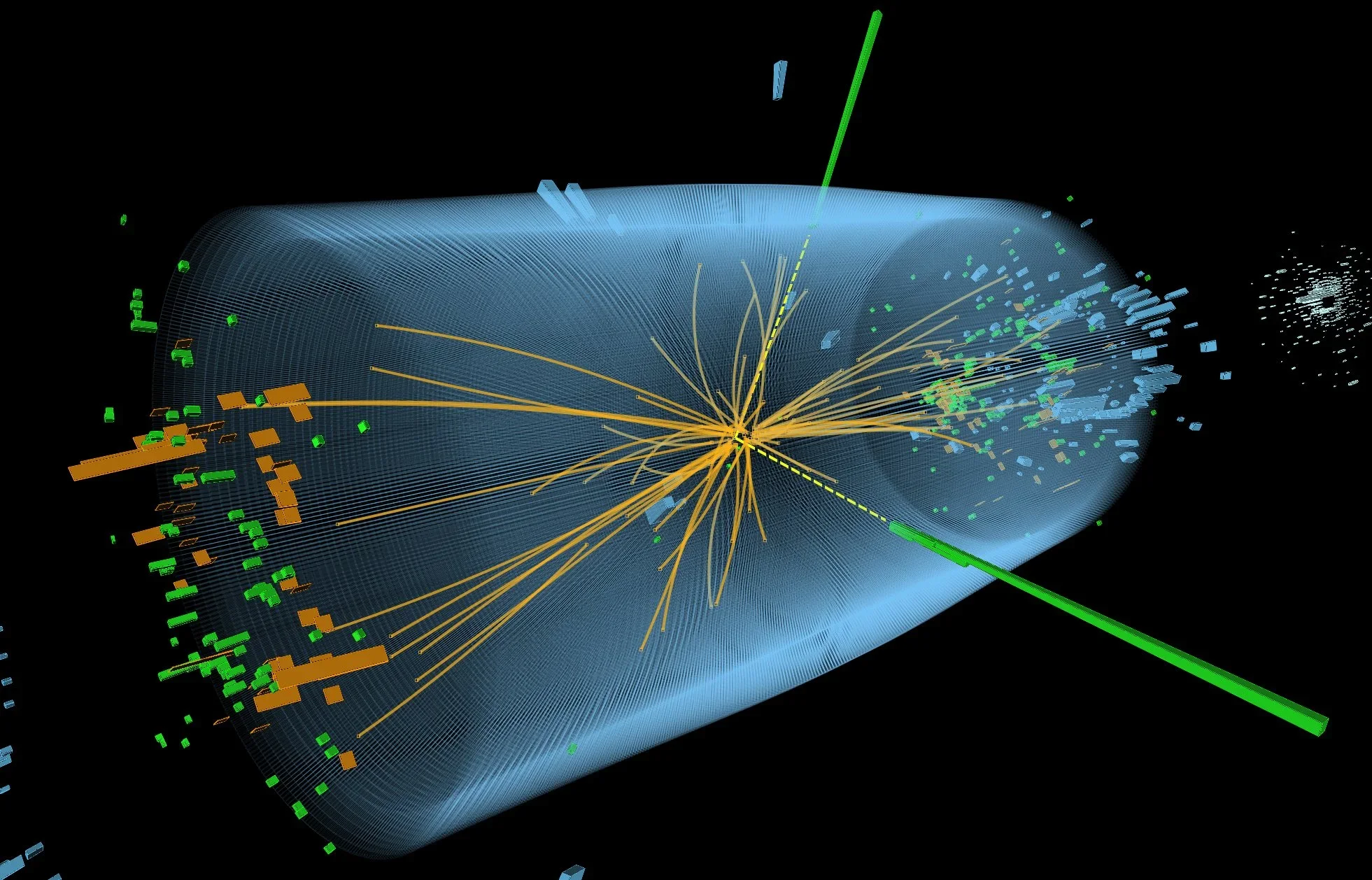
Aquí es donde entra en escena la teoría de cuerdas. En este marco teórico de la física fundamental, las partículas no se describen como puntos, sino como objetos extendidos —cuerdas— que se mueven y vibran en el espacio-tiempo. Las trayectorias de estas cuerdas forman superficies suaves llamadas worldsheets u hojas de universo, cuya forma viene determinada por un principio de mínima acción: la naturaleza prefiere aquellas superficies que minimizan su área.
El hallazgo clave del estudio es que el problema de diseñar una red física con el menor coste material posible es matemáticamente equivalente al problema de encontrar estas superficies mínimas en la teoría de cuerdas. Gracias a esta equivalencia, los investigadores pueden usar herramientas desarrolladas durante décadas en física teórica para predecir cómo deben ramificarse las redes reales.
🗣️ «Parece que existe una regla universal que gobierna la formación de las redes biológicas —afirma Meng. Y añade—: Esta regla de optimización es puramente geométrica. No le importan los tipos de materiales ni las funciones que desempeñan, y resulta ser bastante universal y aplicable a muchos conjuntos de datos diferentes».
Trifurcaciones, brotes ortogonales y redes reales
Cuando se aplica este enfoque, emergen patrones nuevos. Uno de los más importantes es que, a medida que los enlaces de una red se vuelven más gruesos, es decir, cuando la superficie importa más que la longitud, las bifurcaciones clásicas dejan de ser óptimas. En su lugar, aparecen trifurcaciones estables, exactamente como las que se observan en redes reales.
El modelo predice incluso un punto de transición claro: por debajo de cierto grosor, la red se comporta como un conjunto de cables finos; por encima, adopta configuraciones más complejas que minimizan superficie, no longitud.
El mismo razonamiento explica la abundancia de las llamadas ramas ortogonales, esos brotes perpendiculares que surgen de un tronco principal. Lejos de ser anomalías, el modelo demuestra que son soluciones óptimas en un amplio rango de condiciones. Y no solo eso: en muchos sistemas, estas estructuras desempeñan funciones cruciales.
En el cerebro humano, por ejemplo, los investigadores identificaron miles de estos brotes ortogonales en las neuronas. En el 98% de los casos, terminaban en una sinapsis. Es decir, el cerebro aprovecha estas ramificaciones para crear nuevos puntos de conexión con un coste material mínimo, utilizando principios geométricos profundamente ligados a la optimización de superficies. Algo similar ocurre en las raíces de las plantas o en los filamentos de los hongos, donde las ramificaciones perpendiculares permiten explorar el entorno de forma más eficiente.
La teoría de cuerdas, nacida para explicar el origen último del cosmos, se erige como una aliada sorprendentemente eficaz para entender formas de la naturaleza, como son los corales. Foto: Johnny Africa
Soluciones robustas y de bajo coste
El estudio no afirma que la biología use de forma consciente la teoría de cuerdas, ni mucho menos. Pero sí sugiere que las mismas matemáticas que describen objetos fundamentales del universo también gobiernan la forma de las redes naturales, simplemente porque ambas obedecen a principios universales de optimización.
Este enfoque ayuda a resolver un viejo debate: hasta qué punto la forma de las redes biológicas está dictada por la eficiencia material y hasta qué punto por la función biológica.
La respuesta, según los autores, es que la optimización local actúa proporcionando soluciones robustas y baratas, sobre las que luego la evolución y el desarrollo añaden capas funcionales. El resultado final no es el diseño global más corto posible, sino uno que equilibra coste, función y restricciones físicas.
Qué implica este descubrimiento para la ciencia y la ingeniería
Las implicaciones van más allá de la biología. Comprender cómo se organizan las redes físicas podría influir en el diseño de tejidos artificiales, sistemas de transporte, redes energéticas o incluso infraestructuras urbanas. También abre una vía inesperada de diálogo entre disciplinas que rara vez se cruzan: la física teórica más abstracta y el estudio empírico de sistemas naturales.
🗣️ «Estos resultados demuestran y ofrecen un ejemplo fascinante de cómo el instrumental abstracto de la física teórica también puede acercarnos a la resolución de problemas del mundo real, como la exploración y una mejor comprensión de los patrones de conectividad en el cerebro y en las redes vasculares, subraya Gyorgy Korniss, director del Departamento de Física, Física Aplicada y Astronomía del Instituto Politécnico Rensselaer.
En definitiva, el trabajo de Barabási y sus colaboradores propone una idea tan elegante como provocadora: para descifrar el código oculto de las redes naturales, no basta con medir cables; hay que pensar en superficies. Y en ese terreno, la teoría de cuerdas, nacida para explicar el origen último del cosmos, se erige como una aliada sorprendentemente eficaz para entender la forma de un árbol, un coral o una neurona.▪️
Información facilitada por el Instituto Politécnico Rensselaer
Fuente: Meng, X., Piazza, B., Both, C. et al. Surface optimization governs the local design of physical networks. Nature (2026). DOI: https://doi.org/10.1038/s41586-025-09784-4